Beating Prediction Markets with Micro-Edges
A Statistical Walkthrough of a 10/10 Automated Scalping System
Context. I’ve been building a live scalper for binary sports markets on Kalshi. The engine takes +10% profit targets with hard -10% stops, runs a 250 ms risk loop off WebSocket quotes, enters taker (IOC) only when the net edge clears fees, and favors maker-first exits (time-based amend-in-queue degradation targets). Exits/stops are side agnostic: if I’m long YES, I’ll flatten by selling YES or buying NO - whichever book is better right now. Positions are tracked as one net exposure per game, so there’s no self-hedging.
I won’t get into the signals that serve as catalysts for entry trades - that will be for another time.
For now, we will talk about EV, break-even win rate, distribution of session outcomes, and what a Saturday college football slate and session looks like at different true win rates.
The goal = prove this is feasible as a money maker.
The Hypothetical Payoff Model
Bankroll = $400
Stake per pop = $40
Win: +10% → +$4
Loss: -10% → -$4
Friction (fees + tiny slippage): treat it as a per-trade constant F in dollars
Best case (maker-heavy wings): F = $0.50
Blended (my current mix): F = $0.70
Worst case (mid, taker, taker both sides): F = $1.60
Let p = true win probability per trade.
Net EV per trade | EVnet =4(2p−1)−F (dollars)
if p = 0.55: 4(0.10) - F = 0.40 - F
if p = 0.65: 4(0.30) - F = 1.20 - F
if p = 0.75: 4(0.50) - F = 2.00 - F
Break-even win rate (set EV=0) | p⋆=.5+(F/8)
F = 0.50 → p* = 56.25%
F = 0.70 → p* = 58.75%
F = 1.60 → p* = 70.00%
Interpretation: If I hold blended friction near $0.70 per round-trip, I need ~58.8% true hit rate to break even. Keeping exits maker-first and avoiding mis-bucket churn = bar dropping to ~56%.
Variance and confidence bands
Per trade, the random part is ±$4 (fees shift the mean but not volatility).
Per-trade variance: 16p(1-p)
Per-trade stdev: 4sqrt(p(1−p))
Examples:
p = 0.55 = $1.99
p = 0.65 = $1.91
p = 0.75 = $1.73
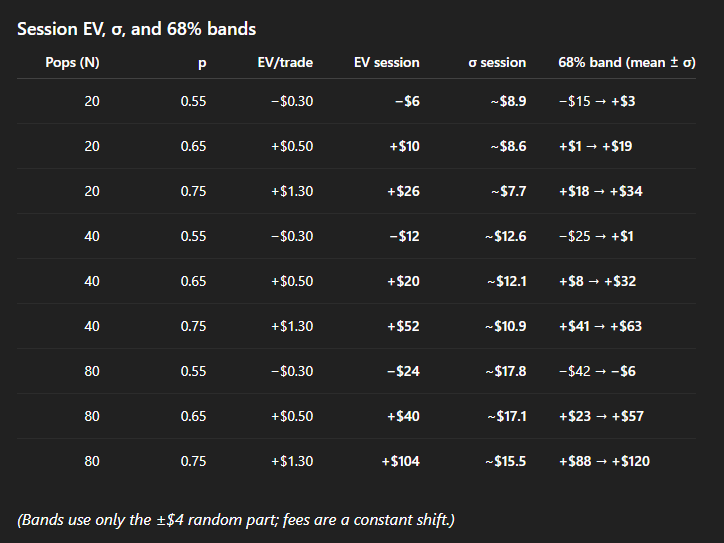
What a Saturday session looks like (bankroll $400, $40 per pop)
Assume I limit concurrent exposure to $40 but re-deploy capital as trades close. Depending on cadence of signals generated, it’s realistic to get anywhere from 20 to 200 pops in a busy college slate.
Let’s use blended friction F = $0.70.
Expected values per trade (blended)
55% → 0.40 - 0.70 = -$0.30
65% → 1.20 - 0.70 = +$0.50
75% → 2.00 - 0.70 = +$1.30
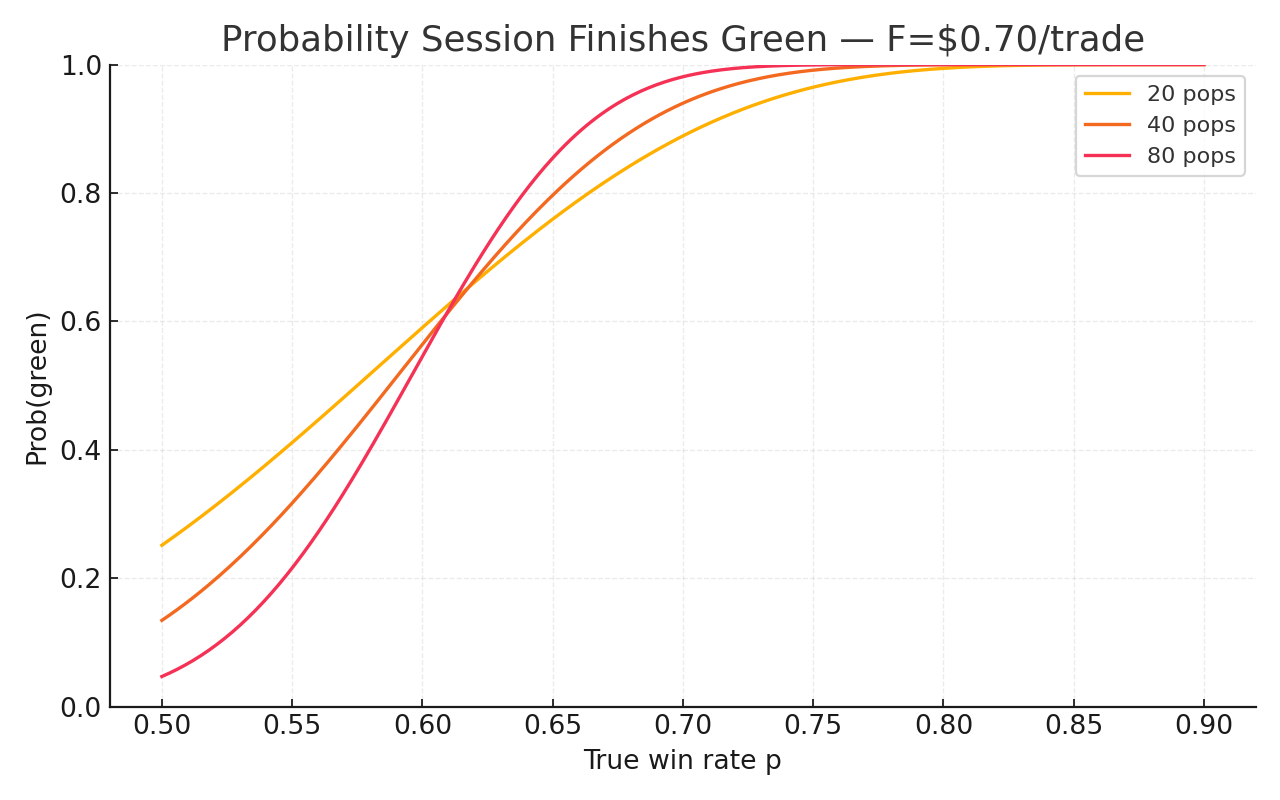
Probability the session finishes green (binomial tatil)
Net PnL > 0 if the wins share exceeds p*. For F = $0.70, p* = 58.75%.
N = 40 pops
p = 0.55: Pr[green] = 32%
p = 0.65: Pr[green] = 80%
p = 0.75: Pr[green] = 99%
N = 80 pops
p = 0.55: Pr[green] = 22%
p = 0.65: Pr[green] = 85%
p = 0.75: Pr[green] = 99.9%
Method: normal approximation to the binomial with continuity correction. Exact binomial yields almost the same numbers here.
Where the win rate comes from and how my code enforces it
This is not a coin-flip p. The engine manufactures win rate by:
Avoiding trades that can’t clear fees
A fee-aware entry-gate exists and rejects any IOC entry whose expected gross < F + slippage + desired net
In code, this is a function of price P and exit style (maker vs taker). It blocks the mid-bucket churners aggressively.
Exiting as maker by default
Maker fees are demonstrably less. The chart below illustrates the divide perfectly.
We must preserve queue priority and shrink F
Fast, deterministic -10% stop
A 250ms risk loop runs entirely off WebSocket quotes - no REST latency - and flips to IOC flatten on whichever side has best liquidity (sell YES or buy NO)
Stops must cross; remove post_only for stops and cross by +1 cent to guarantee fills
One net exposure per game
Track signed exposure per game
Openings may only increase exposure in the current direction; exits/stops can use either side as long as they reduce exposure. No self-hedging, but always route to the better book.
Combined with quality signals (another post to come), this is how you get to 65-75% hit rates with small targets in a fee heavy venue.
Sensitivity: fee control is everything
Every $0.20 in friction shifts break-even by 2.5 percentage points.
Bring exits from taker→maker and skip wide spreads → FFF drops from $0.70 to $0.50 → break‑even drops 58.8% → 56.3%.
Grind in the mid at taker⇄taker → FFF blows out to $1.60 → break‑even jumps to 70%.
Rule: The “10/10” works at 65% with disciplined fee control; it’s a money‑machine at 75%. It fails at 55% unless you operate near‑zero friction (which you won’t in mid‑bucket taker‑land).
Bankroll framing and Kelly Sanity
With $500 and $40 per pop, you’re ~8% Kelly at p=0.65 if you ignore fees (gross “b”=1); with friction, the effective edge is smaller, so the true Kelly fraction is well below 8%.
Practically: $40/pop is conservative enough to tolerate variance, especially when stops are hard and quick. The big benefits are from volume (many small edges) and F control (maker exits).
The punchline
A “10/10” binary scalper is viable if you treat fees as a first‑class constraint and keep the stop hard and fast. With blended friction around $0.70, the break‑even is ~58.8%. That’s reachable when you (i) only take trades that can clear fees, (ii) exit as maker by default, and (iii) stop on a WS‑driven IOC in ≤ 250 ms.
Give me 40–80 pops on a college football Saturday at 65–75% and the math says: +$20 to +$104 expected, with 80–99% odds the session closes green. The edges are small; the discipline is everything.